A massive commonplace deviation signifies that the information points can spread far from the mean and a small commonplace deviation signifies that they are clustered intently around the mean. These identical formulae can be used to obtain confidence intervals on the variance of residuals from a least squares match beneath normal regular principle, where k is now the number of degrees of freedom for error. And the place the integrals are definite integrals taken for x ranging over the set of potential trading tools and indicators values of the random variable X.
Commonplace Deviation And Variance
0 is the smallest value of normal deviation because it can’t be negative. When the weather in a series are extra isolated from the mean, then the usual deviation can additionally be giant. Before finding the variance, we need to discover the imply of the data set. Take the square root of the population variance to get the standard deviation. The following desk lists the boldness intervals comparable to the primary few multiples of the standard deviation (again assuming the info is generally distributed). Using software and programming to calculate statistics is more frequent for bigger units of knowledge, as calculating by hand turns into difficult.
Variance And Commonplace Deviation Method
10.663 lies well within what we’d expect, so whereas there could also be other potential sources of error, the result’s affordable enough that we do not expect error due to our calculations. Standard deviation can additionally be used to predict efficiency tendencies. In investing, for instance, an index fund is designed to replicate a benchmark index. This signifies that the fund will have a low standard deviation from the worth of the benchmark. For a detailed understanding of each of these methods, discuss with the web page above.
- Here are the usual deviation formulation for grouped discrete knowledge by completely different methods.
- Variance and Standard Deviation are the important measures utilized in Mathematics and Statics to find the meaning from a large set of knowledge.
- If all the data values are identical, then it signifies the variance is zero.
- The mathematical impact can be described by the confidence interval or CI.
- The degree of dispersion is computed by the method of estimating the deviation of information points.
What Are The Variance And Normal Deviation?
The normal deviation of an information set, sample, statistical population, random variable, or likelihood distribution is the sq. root of its variance. Standard Deviation is a measure which exhibits how much variation (such as unfold, dispersion, spread,) from the imply exists. The normal deviation signifies a “typical” deviation from the imply. It is a well-liked measure of variability as a end result of it returns to the unique items of measure of the information set. Like the variance, if the information points are near the mean, there is a small variation whereas the info points are extremely spread out from the mean, then it has a excessive variance.
Examples On Variance And Normal Deviation
Standard deviation is the optimistic square root of the variance. Standard Deviation is often abbreviated as SD and denoted by the image ‘σ’ and it tells about how a lot knowledge values are deviated from the imply worth. If we get a low normal deviation then it implies that the values are usually close to the imply whereas a high commonplace deviation tells us that the values are far from the mean value. If the population of curiosity is roughly normally distributed, the standard deviation offers info on the proportion of observations above or beneath sure values.
The Method To Calculate Commonplace Deviation
Together, they’re used to determine whether or not the effects or outcomes of an experiment are statistically important. After entering your knowledge, use the STDEV.S formula in case your knowledge set is numeric or the STDEVA whenever you want to embody textual content or logical values. There are additionally a number of particular formulation to calculate the standard deviation for an entire population.

It helps us understand how spread out the info factors are from the imply, providing a clearer picture of the data’s consistency and reliability. It is broadly used in varied fields, together with statistics, finance, and science, to understand the distribution of data and make knowledgeable selections based on the level of variability present. It is evident to note that each formulas look the identical and have only slide changes in their denominator.
What Does Standard Deviation Tell You?

Standard Deviation is the measure of the variation or dispersion of the given values of the information set. An remark isn’t various commonplace deviations away from the imply. See computational formula for the variance for proof, and for an identical outcome for the pattern commonplace deviation.
The first variable is the value of each point within a knowledge set, with a sum-number indicating every further variable (x, x1, x2, x3, etc). The imply is applied to the values of the variable M and the number of information that is assigned to the variable n. Variance is the typical of the values of squared differences from the arithmetic mean.
Distribution measures the deviation of data from its mean or common place. The degree of dispersion is computed by the tactic of estimating the deviation of information factors. Note that both the formulation for normal deviation comprise what is known as the sum of squares (SS), which is the sum of the squared deviation scores. The calculation of SS is critical so as to determine variance, which in turn is necessary for calculating commonplace deviation. SS is worth noting as a result of in addition to variance and commonplace deviation, additionally it is a component of a number of different statistical measures. In science, normal deviation is usually reported alongside the usual error of the estimate.
Standard deviation is a statistical measure of variability that signifies the common quantity that a set of numbers deviates from their mean. The larger the usual deviation, the more unfold out the values, while a lower normal deviation indicates that the values are usually near the imply. If you take a glance at the distribution of some observed knowledge visually, you can see if the form is comparatively skinny vs. fats. Alternatively, Excel has built-in standard deviation capabilities relying on the info set.
The SD is normally more helpful to describe the variability of the info whereas the variance is often rather more helpful mathematically. For example, the sum of uncorrelated distributions (random variables) also has a variance that is the sum of the variances of these distributions. In science, it’s common to report both the standard deviation of the data (as a abstract statistic) and the usual error of the estimate (as a measure of potential error in the findings).
In this text, we are going to learn about what’s normal deviation, the usual deviation formulation, tips on how to calculate commonplace deviation, and examples of standard deviation intimately. Where μ is the anticipated value of the random variables, σ equals their distribution’s normal deviation divided by n1⁄2, and n is the variety of random variables. The standard deviation therefore is solely a scaling variable that adjusts how broad the curve will be, though it additionally appears in the normalizing fixed. The commonplace deviation of a likelihood distribution is the same as that of a random variable having that distribution. In case of grouped information or grouped frequency distribution, the usual deviation could be found by considering the frequency of data values. According to layman’s words, the variance is a measure of how far a set of data are dispersed out from their imply or average worth.
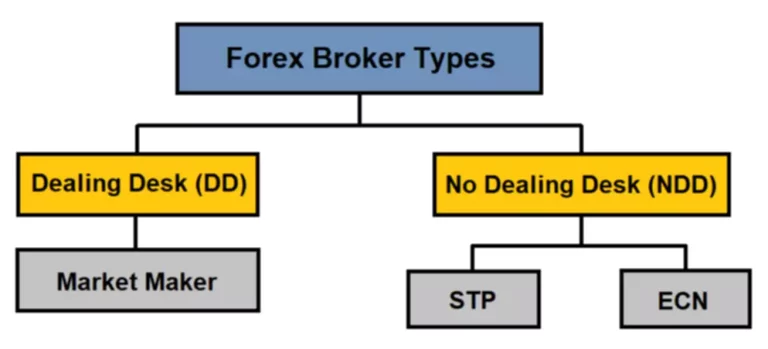
Read more about https://www.xcritical.in/ here.
